10.5 Interference of Light Waves and Young’s Experiment
We will now discuss interference using light waves. If we use two sodium lamps illuminating two pinholes (Fig. 10.11) we will not observe any interference fringes. This is because of the fact that the light wave emitted from an ordinary source (like a sodium lamp) undergoes abrupt phase changes in times of the order of 10–10 seconds. Thus the light waves coming out from two independent sources of light will not have any fixed phase relationship and would be incoherent, when this happens, as discussed in the previous section, the intensities on the screen will add up.
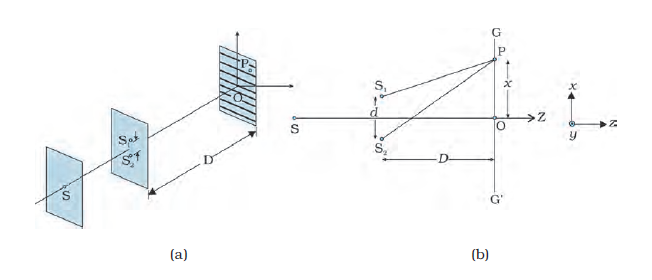
The British physicist Thomas Young used an ingenious technique to “lock” the phases of the waves emanating from S1 and S2. He made two pinholes S1 and S2 (very close to each other) on an opaque screen [Fig. 10.12(a)]. These were illuminated by another pinholes that was in turn, lit by a bright source. Light waves spread out from S and fall on both S1 and S2. S1 and S2 then behave like two coherent sources because light waves coming out from S1 and S2 are derived from the same original source and any abrupt phase change in S will manifest in exactly similar phase changes in the light coming out from S1 and S2. Thus, the two sources S1 and S2 will be locked in phase; i.e., they will be coherent like the two vibrating needle in our water wave example [Fig. 10.8(a)].
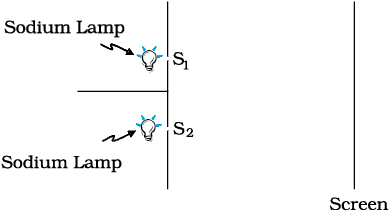
FIGURE 10.11 If two sodium lamps illuminate two pinholes S1 and S2, the intensities will add up and no interference fringes will be observed on the screen.
FIGURE 10.12 Young’s arrangement to produce interference pattern.
Thus spherical waves emanating from S1 and S2 will produce interference fringes on the screen GG′, as shown in Fig. 10.12(b). The positions of maximum and minimum intensities can be calculated by using the analysis given in Section 10.4 where we had shown that for an arbitrary point P on the line GG′ [Fig. 10.12(b)] to correspond to a maximum, we must have
S2P – S1P = nλ; n = 0, 1, 2 ... (10.15)
Now,
(a) (b)
Figure 10.12 Young’s arrangement to produce interference pattern.
(S2P)2 – (S1P)2 =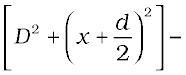 
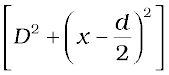= 2x d
where S1S2 = d and OP = x. Thus
S2P – S1P =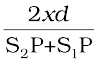 
(10.16)
If x, d<<D then negligible error will be introduced if
S2P + S1P (in the denominator) is replaced by 2D. For example, for d = 0.1 cm, D = 100 cm, OP = 1 cm (which correspond to typical values for an interference experiment using light waves), we have
S2P + S1P = [(100)2 + (1.05)2]½ + [(100)2 + (0.95)2]½
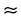200.01 cm
Thus if we replace S2P + S1P by 2 D, the error involved is about 0.005%. In this approximation, Eq. (10.16) becomes
Thomas Young (1773 – 1829)
Thomas Young (1773 – 1829) English physicist, physician and Egyptologist. Young worked on a wide variety of scientific problems, ranging from the structure of the eye and the mechanism of vision to the decipherment of the Rosetta stone. He revived the wave theory of light and recognised that interference phenomena provide proof of the wave properties of light.
S2P – S1P ≈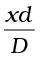 
(10.17)
Hence we will have constructive interference resulting in a bright region when 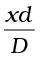= nλ [Eq. (10.15)]. That is,
x = xn =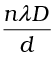 
; n = 0, ± 1, ± 2, ... (10.18)
On the other hand, we will have destructive interference resulting in a dark region whe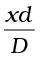n = (n+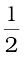
) λ that is
x = xn = (n+)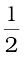 
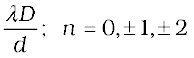(10.19)
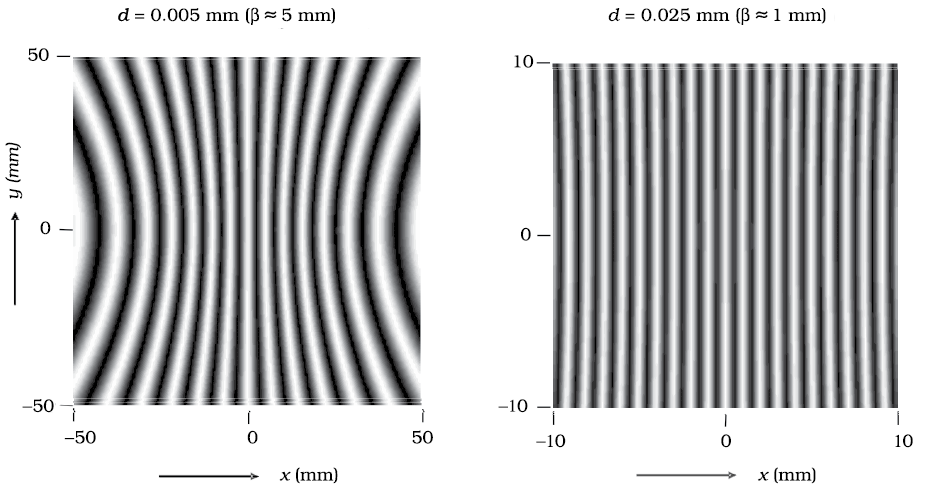
Thus dark and bright bands appear on the screen, as shown in Fig. 10.13. Such bands are called fringes. Equations (10.18) and (10.19) show that dark and bright fringes are equally spaced and the distance between two consecutive bright and dark fringes is given by
β = xn+1 –xn or β =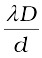 
(10.20)
which is the expression for the fringe width. Obviously, the central point O (in Fig. 10.12) will be bright because S1O = S2O and it will correspond to n = 0 [Eq. (10.18)]. If we consider the line perpendicular to the plane of the paper and passing through O [i.e., along the y-axis] then all points on this line will be equidistant from S1 and S2 and we will have a bright central fringe which is a straight line as shown in Fig. 10.13. In order to determine the shape of the interference pattern on the screen we note that a particular fringe would correspond to the locus of points with a constant value of S2P – S1P. Whenever this constant is an integral multiple of λ, the fringe will be bright and whenever it is an odd integral multiple of λ/2 it will be a dark fringe. Now, the locus of the point P lying in the x-y plane such that S2P – S1P (= ∆) is a constant, is a hyperbola. Thus the fringe pattern will strictly be a hyperbola; however, if the distance D is very large compared to the fringe width, the fringes will be very nearly straight lines as shown in Fig. 10.13.
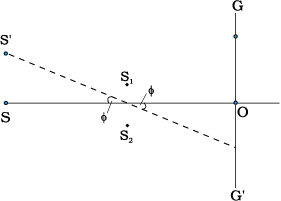
In the double-slit experiment shown in Fig. 10.12(b), we have taken the source hole S on the perpendicular bisector of the two slits, which is shown as the line SO. What happens if the source S is slightly away from the perpendicular bisector. Consider that the source is moved to some new point S′ and suppose that Q is the mid-point of S1 and S2. If the angle S′QS is φ, then the central bright fringe occurs at an angle –φ, on the other side. Thus, if the source S is on the perpendicular bisector, then the central fringe occurs at O, also on the perpendicular bisector. If S is shifted by an angle φ to point S′, then the central fringe appears at a point O′ at an angle –φ, which means that it is shifted by the same angle on the other side of the bisector. This also means that the source S′, the mid-point Q and the point O′ of the central fringe are in a straight line.
We end this section by quoting from the Nobel lecture of Dennis Gabor*
The wave nature of light was demonstrated convincingly for the first time in 1801 by Thomas Young by a wonderfully simple experiment. He let a ray of sunlight into a dark room, placed a dark screen in front of it, pierced with two small pinholes, and beyond this, at some distance, a white screen. He then saw two darkish lines at both sides of a bright line, which gave him sufficient encouragement to repeat the experiment, this time with spirit flame as light source, with a little salt in it to produce the bright yellow sodium light. This time he saw a number of dark lines, regularly spaced; the first clear proof that light added to light can produce darkness. This phenomenon is called interference. Thomas Young had expected it because he believed in the wave theory of light.
*Dennis Gabor received the 1971 Nobel Prize in Physics for discovering theprinciples of holography
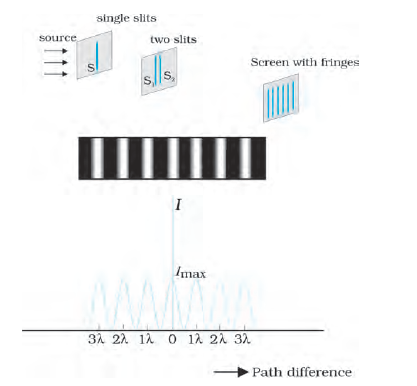
We should mention here that the fringes are straight lines although S1 and S2 are point sources. If we had slits instead of the point sources (Fig. 10.14), each pair of points would have produced straight line fringes resulting in straight line fringes with increased intensities.
Figure 10.14 Photograph and the graph of the intensity distribution in Young’s double-slit experiment.
Example 10.3 Two slits are made one millimetre apart and the screen is placed one metre away. What is the fringe separation when blue-green light of wavelength 500 nm is used?
Solution Fringe spacing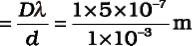 
= 5 × 10–4 m = 0.5 mm
Example 10.4 What is the eff ect on the interference fringes in a Young’s double-slit experiment due to each of the following operations:
(a) the screen is moved away from the plane of the slits;
(b) the (monochromatic) source is replaced by another (monochromatic) source of shorter wavelength;
(c) the separation between the two slits is increased;
(d) the source slit is moved closer to the double-slit plane;
(e) the width of the source slit is increased;
(f) the monochromatic source is replaced by a source of white
light?
(In each operation, take all parameters, other than the one specified, to remain unchanged.)
Solution
(a) Angular separation of the fringes remains constant (= λ/d). The actual separation of the fringes increases in proportion to the distance of the screen from the plane of the
two slits.
(b) The separation of the fringes (and also angular separation) decreases. See, however, the condition mentioned in (d) below.
(c) The separation of the fringes (and also angular separation) decreases. See, however, the condition mentioned in (d) below.
(d) Let s be the size of the source and S its distance from the plane of the two slits. For interference fringes to be seen, the condition
s/S < λ/d should be satisfied; otherwise, interference patterns produced by different parts of the source overlap and no fringes are seen. Thus, as S decreases (i.e., the source slit is brought closer), the interference pattern gets less and less sharp, and when the source is brought too close for this condition to be valid, the fringes disappear. Till this happens, the fringe separation remains fixed.
(e) Same as in (d). As the source slit width increases, fringe pattern gets less and less sharp. When the source slit is so wide that the condition s/S ≤ λ/d is not satisfied, the interference pattern disappears.
(f) The interference patterns due to different component colours of white light overlap (incoherently). The central bright fringes for different colours are at the same position. Therefore, the central fringe is white. For a point P for which S2P –S1P = λb/2, where λb
(≈ 4000 Å) represents the wavelength for the blue colour, the blue component will be absent and the fringe will appear red in colour. Slightly farther away where S2Q–S1Q = λb = λr/2 where λr (≈ 8000 Å) is the wavelength for the red colour, the fringe will be predominantly blue.
Thus, the fringe closest on either side of the central white fringe is red and the farthest will appear blue. After a few fringes, no clear fringe pattern is seen.
