Oscillations : Revision Notes

Not very sure about all the concepts? Revise it all here!

Characteristics of SHM

A restoring force must act on the body.
Body must have acceleration in a direction opposite to the displacement and the acceleration must be directly proportional to displacement.
The system must have inertia (mass).
SHM is a type of oscillatory motion.
It is a particular case of preodic motion.
It can be represented by a simple sine or cosine function

Displacement as a function of time is a simple harmonic motion

Standard equation of simple harmonic motion is:

a = - w^{2} x

Any general equation satisfying the above criterion represents a simple harmonic motion.
i.e.

x = A s i n w t

Velocity as a function of displacement

General equation of SHM for displacement in a simple harmonic motion is:

x = A s i n w t

By definition,

v = \frac{d x}{d t}

or,

v = A w c o s w t

... (1)

Since

s i n^{2} w t + c o s^{2} w t = 1

From equation (1).

v = w A^{2} - x^{2}

Find acceleration from displacement as a function of time

In SHM for displacement has a time dependence equation in the form

x = A s i n w t

By definition,

v = \frac{d x}{d t}

or,

v = A w c o s w t

Acceleration is given by

a = \frac{d v}{d t}

a = - A w^{2} s i n w t

Differential Equation of SHM

\frac{d ^{2} x}{d t} = - w^{2} x

General solution to this equation is:

x = A s i n (w t) + B c o s (w t)

On Putting the boundary conditions specific to the given problem we get:

x = A s i n (w t + δ)

Problem on kinetic energy, potential energy and total energy of a mass attached to a spring in SHM

Example: A mass

m

is attached to a spring of stiffness

k

executing SHM. It has amplitude

A

and velocity at the equilibrium position is

u

. Find the total energy of this spring mass system.

Solution:
At the extreme position of the spring it has only potential energy since velocity is zero:

\frac{k A ^{2}}{2}

At the equilibrium position it has no stretch in the spring.
Kinetic energy at this instant:

\frac{m u ^{2}}{2}

At any instant of time during the motion:
Total energy = KE + PE =

\frac{m u ^{2}}{2}

\frac{k A ^{2}}{2}

Angular Displacement and Angular Velocity of a Physical Pendulum

Angular Displacement of Physical pendulum:

θ = θ_{o} s i n (w t + ϕ)

Angular Velocity of physical pendulum:

ω = θ_{o} w s i n (w t + ϕ)

Write total force and write differential equation of motion for damped oscillations

Total force in damped oscillations is:

c \frac{d x}{d t} + k x

(Due to damper and spring.)

Final differential equation for the damper is:

m \frac{d ^{2} x}{d t ^{2}} + c \frac{d x}{d t} + k x = 0

Displacement as a function of time in damped SHM

x (t) = A c o s (w^{'} t + ϕ) e^{\frac{- b t}{2 m}}

Write force equation and differential equation of motion in forced oscillation

Example: A weakly damped harmonic oscillator is executing resonant oscillations. What is the phase difference between the oscillator and the external periodic force?

Solution:
The equation for forced oscillation in a damped system is given as-

m \frac{d ^{2} x}{d t ^{2}} + b \frac{d x}{d t} + k x = F_{0} c o s ω t

⟹ \frac{d ^{2} x}{d t ^{2}} + 2 β \frac{d x}{d t} + ω_{0}^{2} x = A c o s ω t

The expected solution is of form

x = D c o s (ω t - δ)

Put this is in above equation gives,

t a n δ = \frac{2 β ω}{ω _{0}^{2} - ω ^{2}}

For resonant oscillation,

ω_{0} = ω

⟹ δ = π / 2

which is the phase difference between

x

and

F

Write displacement as a function of time in forced oscillation

The object oscillates about the equilibrium position

x_{0}

. If we choose the origin of our coordinate system such that

x_{0}

= 0

, then the displacement

x

from the equilibrium position as a function of time is given by:

x (t) = A c o s (w t + ϕ)

Oscillations when driving frequency is close to natural frequency

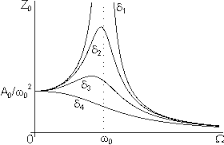
Amplitude of oscillations in shown in the attached plot and given by the formula:

A = \frac{F _{o}}{m _{0}^{2} ( ω ^{2} - ω _{d}^{2} ) ^{2} + ω _{d}^{2} b ^{2}}

where

F_{o} :

Driving Force

m_{o} :

Mass

ω :

Driving Frequency

ω_{d} :

Damping Frequency and

b :

Damping constant

When

ω = ω_{d}

, amplitude of oscillations is maximum.

A = \frac{F _{o}}{ω _{d} b}

which is a very large value.

This is the phenomenon of resonance in forced oscillations.

Facebook SDK (Plugin)

Oscillations : Revision Notes

Characteristics of SHM

Displacement as a function of time is a simple harmonic motion

Velocity as a function of displacement

Find acceleration from displacement as a function of time

Differential Equation of SHM

Problem on kinetic energy, potential energy and total energy of a mass attached to a spring in SHM

Angular Displacement and Angular Velocity of a Physical Pendulum

Write total force and write differential equation of motion for damped oscillations

Displacement as a function of time in damped SHM

Write force equation and differential equation of motion in forced oscillation

Write displacement as a function of time in forced oscillation

Oscillations when driving frequency is close to natural frequency

Made with Love by

Contact form

Facebook SDK (Plugin)

Oscillations : Revision Notes

Characteristics of SHM

Displacement as a function of time is a simple harmonic motion

Velocity as a function of displacement

Find acceleration from displacement as a function of time

Differential Equation of SHM

Problem on kinetic energy, potential energy and total energy of a mass attached to a spring in SHM

Angular Displacement and Angular Velocity of a Physical Pendulum

Write total force and write differential equation of motion for damped oscillations

Displacement as a function of time in damped SHM

Write force equation and differential equation of motion in forced oscillation

Write displacement as a function of time in forced oscillation

Oscillations when driving frequency is close to natural frequency

You may like these posts